
Magical Multiplication: Simple Strategies to Love Learning Your Times Tables
Table of Contents
Multiplication may seem like a daunting aspect of mathematics, but with the right approach, it becomes more of an exciting adventure than a chore. When we view multiplication as “magical multiplication,” it becomes an intriguing process that is easy to grasp, especially for beginners. This key skill is foundational to numerous areas of mathematics and beyond, making it essential for new learners to become comfortable with early on.

We understand that it’s not just about memorising times tables; it’s also about recognising patterns and relationships between numbers. From utilising addition to multiply, to tricks with zeroes and ones, there are various strategies that can simplify the learning process. By engaging with multiplication through practical application and fun activities, the journey from beginner to proficient is filled with discovery and accomplishment.
Key Takeaways
- Multiplication is a foundational skill made exciting with the right approach.
- Various strategies and patterns ease the learning process.
- Engaging with fun activities deepens understanding and proficiency.
Understanding Multiplication Basics
Before diving into the intricate world of multiplication, we need to grasp its fundamentals: what multiplication is and the essential roadmap – the multiplication table.
Defining Multiplication
Multiplication is a simple mathematical operation where we combine equal groups to find a total. Think of it as speedy repeated addition. For example, when we multiply 2 by 3, it’s the same as adding 2 three times (2 + 2 + 2).
The Multiplication Table
The multiplication table, or times tables as we often call them, is a structured grid of numbers that helps us quickly find the result when we multiply two numbers. Each cell in the table represents the product – the result of our multiplication. It’s vital for beginners to familiarise themselves with this table, as it lays the groundwork for mastering multiplication. Here’s a segment of the table for reference:
| x | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 1 | 1 | 2 | 3 | 4 | 5 |
| 2 | 2 | 4 | 6 | 8 | 10 |
| 3 | 3 | 6 | 9 | 12 | 15 |
| 4 | 4 | 8 | 12 | 16 | 20 |
| 5 | 5 | 10 | 15 | 20 | 25 |
By learning and practising these tables, we can quickly and efficiently multiply numbers without relying on calculators or long-winded counting.
Learning the Times Tables
To establish a solid foundation in mathematics, we must ensure a strong grasp of the times tables. They are fundamental to understanding more complex mathematical concepts. Therefore, mastering them is not just about memorisation—it’s about developing confidence and speed in arithmetic.
Memorisation Techniques
Memorisation of multiplication facts is key to mastering the times tables. One effective method is rote memorisation, which involves repeated practice of the times tables until they are committed to memory. For instance, we might start by focusing on the 2-times table, repeating it out loud or writing it down multiple times. Here’s a simple format we could use for the 2-times table:
| 1 x 2 | = 2 |
|---|---|
| 2 x 2 | = 4 |
| 3 x 2 | = 6 |
| 4 x 2 | = 8 |
| … | … |
After becoming comfortable with one table, we can move on to the next, ensuring we are able to recall each fact rapidly and accurately.
Times Tables Games
Incorporating games into our practice can make learning more engaging. Times tables games transform what might be seen as a tedious task into a fun and interactive way to reinforce multiplication facts. From online resources like LearningMole, which offers a variety of educational games and activities, to simple card games that we can play with friends or family, turning learning into play is a fantastic way to enhance our mathematical journey. Games allow us to apply what we’ve memorised in different scenarios, enhancing our understanding and recall.
Addition and Multiplication
We often consider addition and multiplication as fundamental operations in mathematics. It’s essential to understand how these two are interconnected and how the distributive property plays a significant role in these operations.
Connection Between Addition and Multiplication
Addition is the process of combining two or more numbers to find a total or a sum. For example, if we have 2 apples and we add 3 more, we now have 5 apples. Multiplication, on the other hand, is a shortcut for repeated addition. If we want to add the number 3 five times (3+3+3+3+3), we can express this as 3 multiplied by 5, or 3×5, which equals 15.
This reveals an intrinsic link between the two operations: multiplication is essentially adding the same number repeatedly. Understanding this relationship helps us to form fact families, where the same numbers can be regrouped to show both addition and multiplication. For example, from the fact family of 2, 3, and 6, we know that 2+2+2=6 and 2×3=6.
Distributive Property of Multiplication
The distributive property refers to the way multiplication interacts with addition and is a crucial concept in algebra. This property states that multiplying a sum by a number gives the same result as multiplying each addend by the number and then adding those products. For instance, 2×(4+3) is the same as (2×4) + (2×3).
In practical terms, if we want to buy 2 sets of pencils, with each set containing 4 blue and 3 red pencils, we could find the total by first adding 4 and 3 to calculate the number of pencils in one set, then multiplying by 2, which is 14 pencils.
Conversely, we could multiply 2 by 4 (for the blue pencils) and 2 by 3 (for the red pencils), then add the results, which also gives us 14 pencils. Both methods utilise the distributive property to reach the same solution.
Multiplying with Zeroes and Ones
In this section, we’re going to explore the special rules when you multiply with zero and one, alongside practical examples to help you understand these concepts better.
Unique Rules for Zero and One
When we tackle multiplication involving the numbers zero and one, it’s crucial to remember these distinct properties:
- Multiplying by zero: Any number multiplied by zero gives a product of zero. This rule is absolute, no matter what number you start with.
- Multiplying by one: If you multiply any number by one, the product is the original number itself; essentially, the number remains unchanged.
These properties stem from the basic rules of multiplication and the idea that multiplication is repeated addition. If we have zero groups of a number, there’s nothing to add, so the result is zero. Whereas, if we have just one group of a number, it’s simply the number itself.
Practical Examples
To illustrate how these rules are applied in practical situations, let’s look at a couple of examples:
-
2 multiplied by 0: Here, we have two groups of zero. Since there’s nothing to add, our answer is simply 0.
-
7 multiplied by 1: This time, we have one group of seven, so our answer doesn’t change, and we get 7.
It’s our goal to make the journey of learning as engaging as possible. Multiplication with zeroes and ones might seem like straightforward concepts, but they form the bedrock of more complex mathematical operations. By mastering these fundamental rules, we’re setting a strong foundation for tackling more challenging problems with confidence.
Practising Multiplication with Objects
By engaging with everyday items, learners can translate abstract multiplication concepts into concrete experiences. Our hands guide us, physically manipulating objects to solve multiplication problems and grounding our understanding in practically-based maths.
Using Everyday Objects
We can start by gathering common household items such as buttons, pebbles, or dried beans. For example, we may want to solve a multiplication problem like 4 x 3. We’ll take 4 groups of 3 objects and arrange them so that we have 4 rows with 3 beans in each row.
This visual and tactile process helps to illustrate that 4 multiplied by 3 equals 12, as we can count the beans to find the answer. In traditional schooling, we often abstract math into symbols and numbers on a page; however, by using tangible objects, we transform numerals into actual quantities that we can see and touch.
Importance of Hands-On Activities
Discovering the value of hands-on activities for learning multiplication is pivotal. When learners interact with physical objects, they engage multiple senses which aid in memory retention and conceptual understanding. It’s vital that we give children the opportunity to experiment with and manipulate objects, reinforcing their maths skills through practice that feels more like play.
Such kinesthetic learning activities support the idea that education should be as immersive and enjoyable as possible, a notion that is at the heart of innovative education platforms such as LearningMole. Through practical handling and experimentation, abstract multiplicative relationships become concrete, fostering both confidence and competence in young mathematicians.
Double and Triple Times
In this section, we’re exploring some simple multiplication tricks that make working with numbers, specifically doubles and triples, a breeze.
Doubling Numbers
When we talk about doubling, we’re simply multiplying a number by two. It’s one of the essential multiplication tricks we can use. For instance, the doubles fact for 4 is 8 because 2 x 4 equals 8. Here’s a quick list to help recognise these patterns:
- 1 x 2 = 2
- 2 x 2 = 4
- 3 x 2 = 6
- 4 x 2 = 8
- 5 x 2 = 10
By committing these to memory, we’re essentially seeing double effortlessly, which speeds up our mental math!
Working with Triples
Tripling, similarly, is when we multiply a number by three. It involves looking at groups of three and understanding how to quickly and efficiently calculate these amounts. Take a look at these examples:
- 1 x 3 = 3
- 2 x 3 = 6
- 3 x 3 = 9
- 4 x 3 = 12
- 5 x 3 = 15
Our ability to multiply in double and triple times enhances dramatically with just a bit of practice and the use of these simple but effective techniques.
Fun with Fives and Tens
In this section, we’re going to explore the simplicity and efficiency of the fives and tens times tables, which are the stepping stones to mastering multiplication.
Fives Times Table Made Easy
When we look at the fives times table, we notice a delightful pattern: the unit’s place is always alternating between 5 and 0. It’s easy to remember, and with this pattern, we can quickly find any multiple of five. If we’re multiplying 5 by an even number, the product ends in 0, and if it’s an odd number, the product ends in 5. Here’s a quick reference:
| Multiplication | Product |
|---|---|
| 5 x 1 | 5 |
| 5 x 2 | 10 |
| 5 x 3 | 15 |
| 5 x 4 | 20 |
| 5 x 5 | 25 |
| … | … |
The Magic of Multiplying by Ten
For the 10 times table, the magic is in the tens place. All you need to do is add a zero to the number you’re multiplying by ten. This rule holds true no matter how large the number, making it one of the simplest multiplication facts to remember.
| Multiplication | Product |
|---|---|
| 10 x 1 | 10 |
| 10 x 2 | 20 |
| 10 x 3 | 30 |
| 10 x 4 | 40 |
| 10 x 5 | 50 |
| … | … |
By using these easy strategies, we can confidently solve multiplication problems involving fives and tens, and understand the multiples of these numbers without hesitation. Whether we’re working on homework or calculating in our daily lives, these methods are not just useful—they’re a lot of fun too!
Exploring Even and Odd Numbers
When we begin to explore the intriguing world of numbers, understanding the difference between even and odd numbers is fundamental. These two types of numbers have unique properties that are essential in the realm of multiplication.
Multiplying with Even Numbers
An even number is any integer that can be divided by two without leaving a remainder. For instance, numbers such as 2, 4, and 6 are even because they can be perfectly divided into pairs. When we multiply two even numbers, the result is always even. Consider the following table:
| Even Number | Multiplied By | Result | Even? |
|---|---|---|---|
| 2 | 4 | 8 | Yes |
| 6 | 2 | 12 | Yes |
| 8 | 6 | 48 | Yes |
This property of even numbers is reliable, making calculations predictable and less complex, particularly for beginners.
Challenges of Odd Numbers
In contrast, an odd number cannot be divided evenly by two; it always leaves a remainder of one. Odd numbers, such as 1, 3, and 5, offer distinct multiplication challenges. When multiplying an odd number with an even number, the product is always even, whereas multiplying two odd numbers together results in an odd product:
| Odd Number | Multiplied By | Result | Odd? |
|---|---|---|---|
| 3 | 2 | 6 | No |
| 5 | 5 | 25 | Yes |
| 7 | 4 | 28 | No |
We must pay close attention when multiplying odd numbers together. The patterns are not as straightforward as with even numbers, requiring us to be vigilant and validate our results to avoid mistakes.
Advanced Techniques
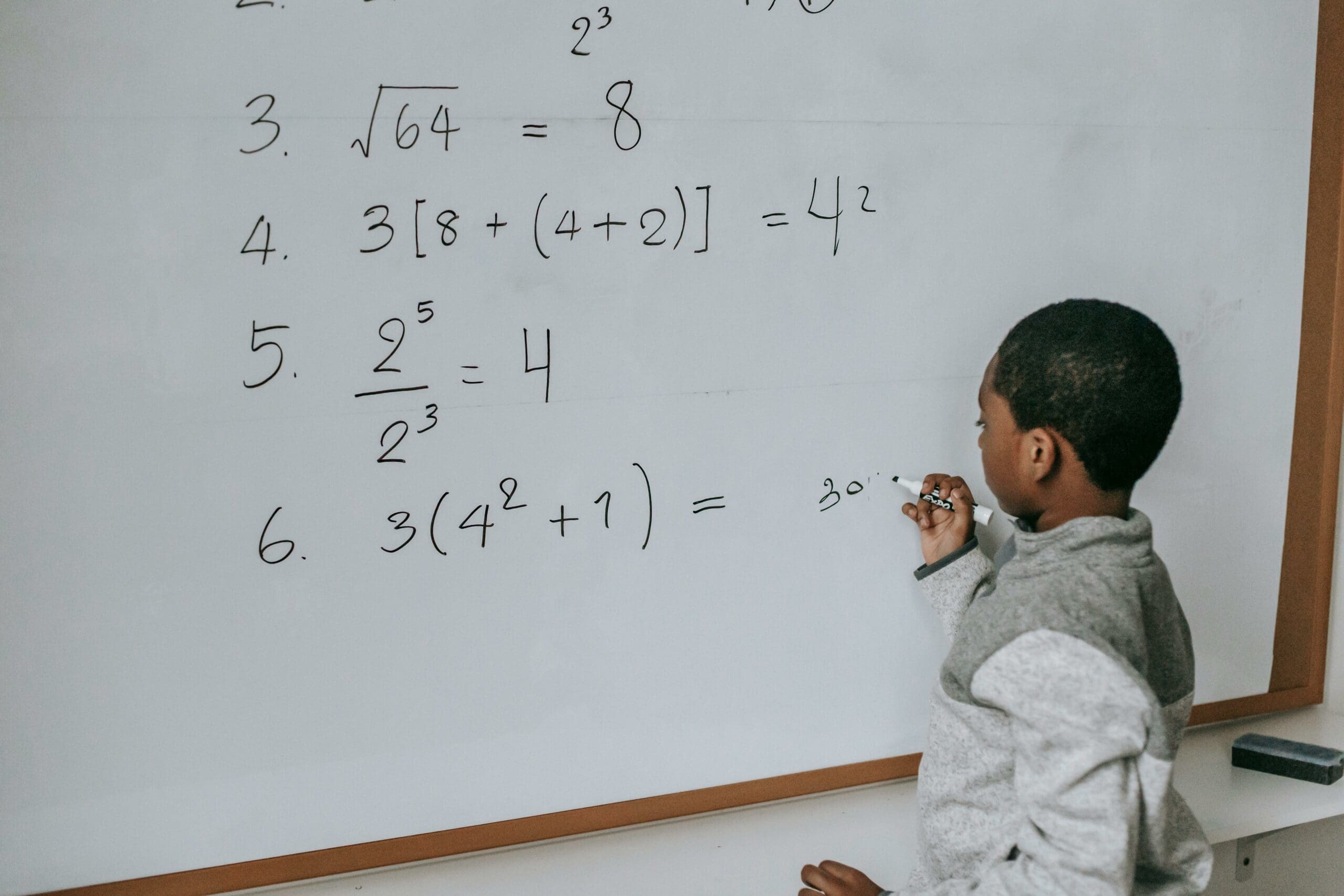
In this section, we’re going to focus on two sophisticated techniques to level up your multiplication skills: dealing with squares and powers, as well as efficiently multiplying two-digit numbers. These methods will enhance your speed and calculation abilities significantly.
Squares and Powers
When we talk about squares, we’re referring to the result of multiplying a number by itself. To square any two-digit number ending in 5, there’s a quick trick we can employ. Take the first digit and multiply it by one higher number, then simply append 25 to the result. For example, to square 35, we multiply 3 by 4 (the next higher number) to get 12, and then add 25 at the end to get 1,225.
For other squares and powers, one can utilise patterns and shortcuts. For instance, when squaring numbers close to 50, it’s useful to remember that 50 squared is 2,500. If we’re squaring a number like 48, we can subtract 2 from 50, square that difference getting 4, subtract that from 2,500, and then subtract the last digit squared (which is 4 in this case), ending up with 2,304.
Multiplying Two-Digit Numbers
Multiplying any two-digit number by another can be accomplished with cross multiplication. This is especially useful for numbers where the tens place is the same and the units place adds up to 10. Consider 23 x 27. Since the tens figure is the same, we multiply 2 (20s) by 3 (the next number in line), which gives us 60, and we multiply the units (3 x 7) to get 21. Combining these we have 621.
For numbers not fitting such patterns, we break them down into tens and units, multiply each part separately, and then add the results. As with method before, always double-check your final digit. If we are multiplying, let’s say, 34 by 82, we multiply 30 by 80 (2400), 30 by 2 (60), 4 by 80 (320), and lastly, 4 by 2 (8). Adding them together gives us 2788.
By mastering these advanced techniques, you’ll be able to multiply larger numbers more quickly and with greater accuracy. Remember, practice makes perfect!
Games and Activities for Mastery
To truly master multiplication, engagement with the material in a fun and interactive way is essential. We find that games and activities solidify understanding and make learning multiplication an enjoyable experience.
Interactive Math Games
Math activities online can transform the way we learn multiplication. At LearningMole, we offer various interactive math games that cater to individual learning paces and styles. These games include challenges that adapt to a child’s level of proficiency, ensuring that they always feel suitably challenged and motivated. With vibrant graphics and intuitive gameplay, our math games make mastering the times tables both exciting and rewarding.
Group Learning Activities
In group learning activities, children experience the power of collaborative learning. Working in small groups, they tackle multiplication games and solve problems together. This peer learning approach not only enhances their multiplication skills but also fosters social interaction and teamwork.
At LearningMole, we provide resources like printable multiplication games activities, where children can pair up or work in teams to compete in a friendly and educational environment. These activities are designed to be hands-on, promoting active participation and making the learning process vivid and memorable.
Frequently Asked Questions
In this section, we’ll address some common queries related to easy multiplication methods, with a focus on tricks that are both quick to learn and fun for beginners.
What are some quick methods to multiply numbers in your head?
One effective way to multiply numbers in your head is by using the ‘split and combine’ method, where you break down one of the numbers into smaller, more manageable parts, multiply each part separately, and then add the results together. For example, to multiply 14 by 3, you could multiply 10 by 3 and 4 by 3, then sum the two products.
Can you provide any tricks to help with multiplying numbers 6 through 9?
Yes, the finger multiplication method is a popular trick for numbers 6 through 9. Bend the finger that corresponds to the number you want to multiply by 6, 7, 8, or 9, and then count the fingers, including the bent one, for your answer.
What techniques can make multiplying large numbers simpler?
For multiplying larger numbers, you can use the grid or lattice method, where you draw a grid and allocate each digit of the numbers in separate rows and columns, then multiply and add accordingly. This visual approach simplifies the process and minimizes errors.
Where can I find a guide to learn multiplication tricks in PDF format?
There are online resources available, such as this guide, that provide a PDF format document filled with techniques and tricks to learn multiplication in an easy-to-follow manner.
How can you easily multiply two-digit numbers using shortcuts?
The cross-multiplication method is a shortcut for two-digit numbers. First, multiply the tens digits of both numbers, then cross-multiply and add the results, and finally multiply the units digits. Combine these results to get your final answer.
What are some fun multiplication strategies for children?
Children respond well to fun and interactive strategies like multiplication games, rhymes, and storytelling. Visual aids such as colourful charts and flashcards also make the learning process more engaging for young learners.


Leave a Reply