
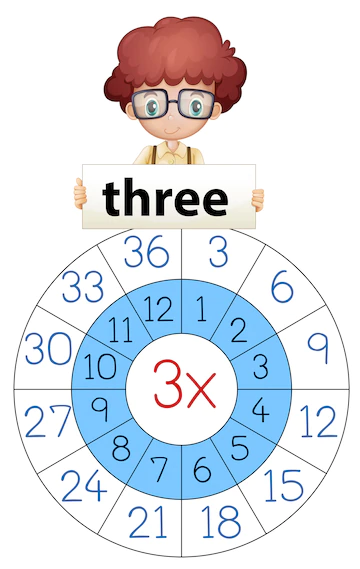
Multiplication Times Tables – 3x Magic Tables
A fun animated math video to help your child learn the times tables or multiplication facts. The three times table is in this video to help your child with their times tables practice.
The First Step of Learning Multiplication
The first step in learning how to multiply is to know about the times tables because they act like the fact sheet for multiplication.
All the numbers could be multiplied by one another, the thing is that some are easy to multiply in mind and by hand while others will need specific methods which will make it easier for the kids to bring out the answers and these are usually used with the bigger numbers.
The First Step of Teaching Kids
The first step in teaching kids multiplication times tables is giving them the chance to understand it all and know how the answers are counted, and then parents should go a little bit further and help the kids to memorize the times tables in an easy way through using any kind of creative ideas.

This is considered important because when kids understand how the times tables are counted, they become more able to bring a specific answer to two numbers multiplied by one another If they forgot it while they are exposed to the question.
Multiplication
Multiplication is the same as double adding and there are also some other words used in the multiplication vocabulary that would tell the kids what they are supposed to do.
Double adding means adding the number which the kid is learning to every answer he/she gets in order to reach the one coming next.
For example, if you are teaching your kid the times table of number 3 then they will find out that 3 x 1 = 3 and thus 3 x 2 = 6 because they will add 3 to the 3 they got in the first equation, and so on.
Would you like to know more about timetables? Come and check our timetables articles: x10 Magic Tables, x9 Magic Tables, x8 Magic Tables, x7 Magic Tables, x6 Magic Tables, x5 Magic Tables, x4 Magic Tables and x2 Magic Tables.
Why not subscribe to our LearningMole Library for as little as £1.99 per month to access over 1400 fun educational videos.


Leave a Reply