
The Amazing 5 Even Numbers
Introducing Even and Odd Numbers
Identifying even and odd numbers is an important skill that children need to help them understand our number system and aid in their preparation to group whole number operations. It will also help prepare them to learn division, prime numbers, and even square roots.
Some kids really struggle with understanding even and odd numbers. This concept is important because it helps the student see a pattern within the numbers. It is a precursor for skip counting, division, and prime numbers. So, making sure kids understand this early on is important.
Even Numbers are integers that are divisible by 2, with no remainders. This means that the number can be divided into pairs or two equal groups with no leftovers. The examples of even numbers are 2, 6, 10, 20, 50, etc.
What is the Even Number In Math?
A number that can be divided into two halves, i.e. into two equal parts. That is called an even number. In other words, even numbers are exactly divisible by 2. Which means that the remainder will be 0.
What are Even Numbers in General?
Whole numbers that have the digits 0, 2, 4, 6, or 8 in there one’s place are even numbers. Even numbers always end up with the last digit as 0, 2, 4, 6, or 8. Some examples of even numbers are 2, 4, 6, 8, 10, 12, 14, and 16.
These are even numbers as these numbers can easily be divided by 2. It should be noted that the smallest positive even natural number is 2. If you pick a number that cannot be divided by 2,
it will be known as an odd number For Example- 1, 3, 5, 7, 9, etc.
How to Know if a Number is Even or Odd?
To find out whether the given number is odd or even, you need to check the number in one’s (or unit’s) place. That particular number in one’s place will tell you whether the number is odd or even.
- Even numbers end with 0, 2, 4, 6, 8
- Odd Numbers end with 1, 3, 5, 7, 9
If the unit’s digit (or one’s digit) is 1, 3, 5, 7, or 9, then the number is called an odd number. If the unit’s digit is 0, 2, 4, 6, or 8, then the number is called an even number. These are the simple tricks to identify the numbers whether they are even or odd.
Think about the following numbers 3, 845, and 917 which end with an odd number i.e. 3, 5, and 7. Therefore, the given numbers 3, 845, and 917 are odd numbers. Thus, those numbers are not even numbers. In the same way, 8 and 322 are even numbers as they end with 8 and 2.
Zero
Zero is an even number because there is nothing to pair and nothing is left over. So, it means it is even. For mathematicians, zero is an even number because any number that can be divided by two to create another whole number is even. Zero passes this test because if you halve zero you get zero. We should memorize 0,2,4,6,7, and 8 as even and 1, 3,5,7, and 9 as odd.
List of Even Numbers up tp 100
The even numbers’ list up to 100 is given below:
2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40, 42, 44, 46, 48, 50, 52, 54, 56, 58, 60, 62, 64, 66, 68, 70, 72, 74, 76, 78, 80, 82, 84, 86, 88, 90, 92, 94, 96, 98, 100
Properties of Even Numbers
Property of Addition
There are three important properties of even numbers which are given below: Adding an even and another even number will always result in an even number
Example: Even + Even = Even, 14 + 6 = 20
Property of Subtraction
Subtracting an even number from another even number will always result in an even number.
Example: Even – Even = Even, 16 – 6 = 10
Property of Multiplication
Multiplying an even number with another even number will always result in an even number.
Example: Even × Even = Even, 6 × 4 = 24
Summary of Facts
The sum of two or more even numbers is always even
Even numbers when divided by 2 leave no remainder
Even numbers are multiples of two
There are no remainder. Yes, it’s true!
Even numbers when multiplied by any number always result in an even number
The product of two or more even numbers is always even
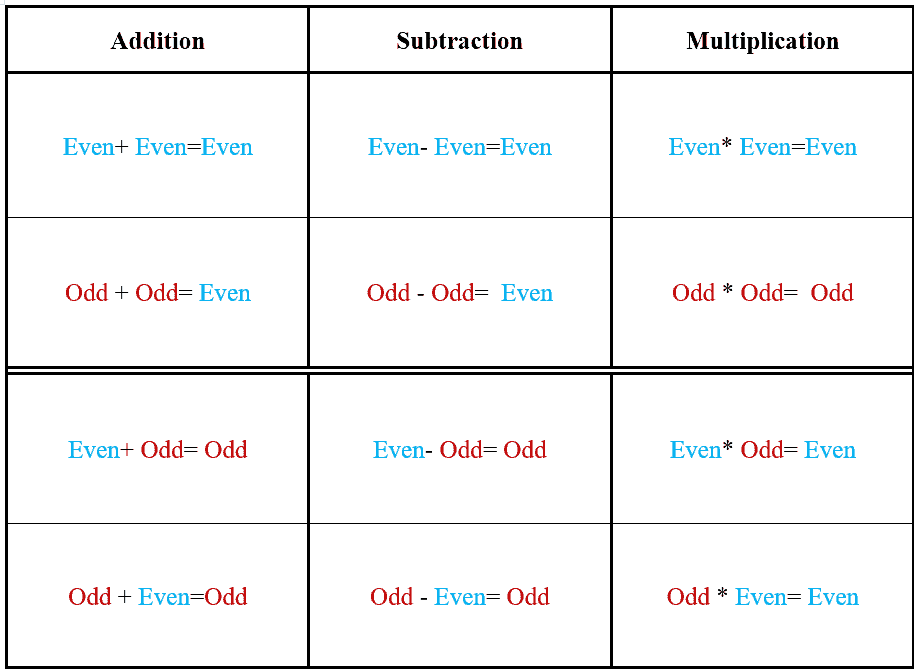
The Property of Addition
- When adding an even number and an odd number (or vice-versa), the resulting number will always be an odd number.
Examples:
9 + 4 =13
3 + 20 =23
Adding an even number and another even number, will result in a number that is always even.
Examples:
14+6 =20
Adding an odd number and another odd number, will always be resulting in a number that is even.
Examples:
11 + 13=24
The Property of Subtraction
- If you subtract an even number from an even number, the answer is an even number
- If you subtract an odd number from an odd number, the answer is an even number
- If you subtract an even number from an odd number, the answer is an odd number
- If you subtract an odd number from an even number, the answer is an odd number
- Subtracting an even number from an odd number (or vice-versa), will result in a number that is always odd.
Examples:
7 – 4= 3
8 – 5= 3
Subtracting an even number from another even number, will result in a number that is always even.
Example:
12 – 8= 4
Subtracting an odd number from another odd number, will result in a number that is always even.
Examples:
23 –11 = 12
The Property of Multiplication
Multiplying an even number and another even number will always result in an even number.
Examples:
8 × 2= 16
10 × 6= 60
Multiplying an even number and an odd number will always result in an even number.
Examples:
4 × 5= 20
8 × 5= 40
Multiplying an odd number and another odd number will always give you an odd number.
Examples:
3 × 5= 15
3 × 5= 15
Even numbers between 40 and 60
Let us have a look at the list of even numbers between 40 and 60. 42, 44, 46, 48, 50, 52, 54, 56, 58 Thus, there are a total of 9 even numbers between 40 and 60. Go through the examples and solutions of the even number given below for a better understanding.
Example 1:Some Even Numbers Solved Problems
Are all whole numbers even?
Solution:
No, the list of whole numbers which are exactly divisible by two is called the even numbers.
Example 2:Write any four consecutive even numbers between the numbers 13 to 21.
Solution:
Let A = {13, 14, 15, 16, 17, 18, 19, 20, 21}
Therefore, 14, 16, 18, 20 are 4 consecutive even numbers.
Example 3:
Choose the correct answer. The sum of two even numbers
A) Is always an even number
B) Is always an odd number
C) is sometimes odd and sometimes even
d) Maybe neither odd nor even Solution:
The correct answer is option a). Even number + Even number = Even number
Example 4: −24, 0, 6, and 38 are all even numbers?
Yes, all numbers -24, 0, 6, and 38 are even numbers.
Example 5: Is 2 an even number?Yes, 2 is an even number since 2 is exactly divisible by 2.
Example 6: What are the even numbers between 1 and 50?The list of even numbers between 1 and 50 are: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40, 42, 44, 46, 48
Example 7: Which is the even prime number?2 is the only even prime number.
Example 8: If you add two even numbers together, the answer is:
- Always even
- Always odd
- Sometimes even and sometimes odd
- 0
- Even + Even = Even For Example, 2 + 6 = 8. So, the answer is always even.
Example 9: Which one of the following is even?
- 9 × 14
- 15 ×17
- 17 × 9
- 11 ×19
9 × 14=126 is even because odd × even = even 15 × 17=255 is odd because odd × odd = odd 17 × 9=153 is odd because odd × odd = odd 11 × 19=209 is odd because odd × odd = odd
so, the answer is A.
Example 10: Which one of the following is even?
a.5+16 b.22+12 c.13+44 d.11+4The answer is b. Why?
How do you write the general form of an even number?
The general form of an even number is 2k, where k is an integer.
Worksheets on Even Numbers
- What are the even numbers from 1 to 100?
- How to know if a number is even?
- Can you guess the first even number?
- Name the smallest even number?
This was all about Even Numbers. We hope you enjoyed it. To practice even more on even numbers and learn about other interesting mathematics’ concepts, keep visiting LearningMole.


Leave a Reply