Numbers are the language of mathematics, as they are used to express quantities and they are the basis of mathematics on which arithmetic operations are performed daily. Such as calculating days, months, or years.
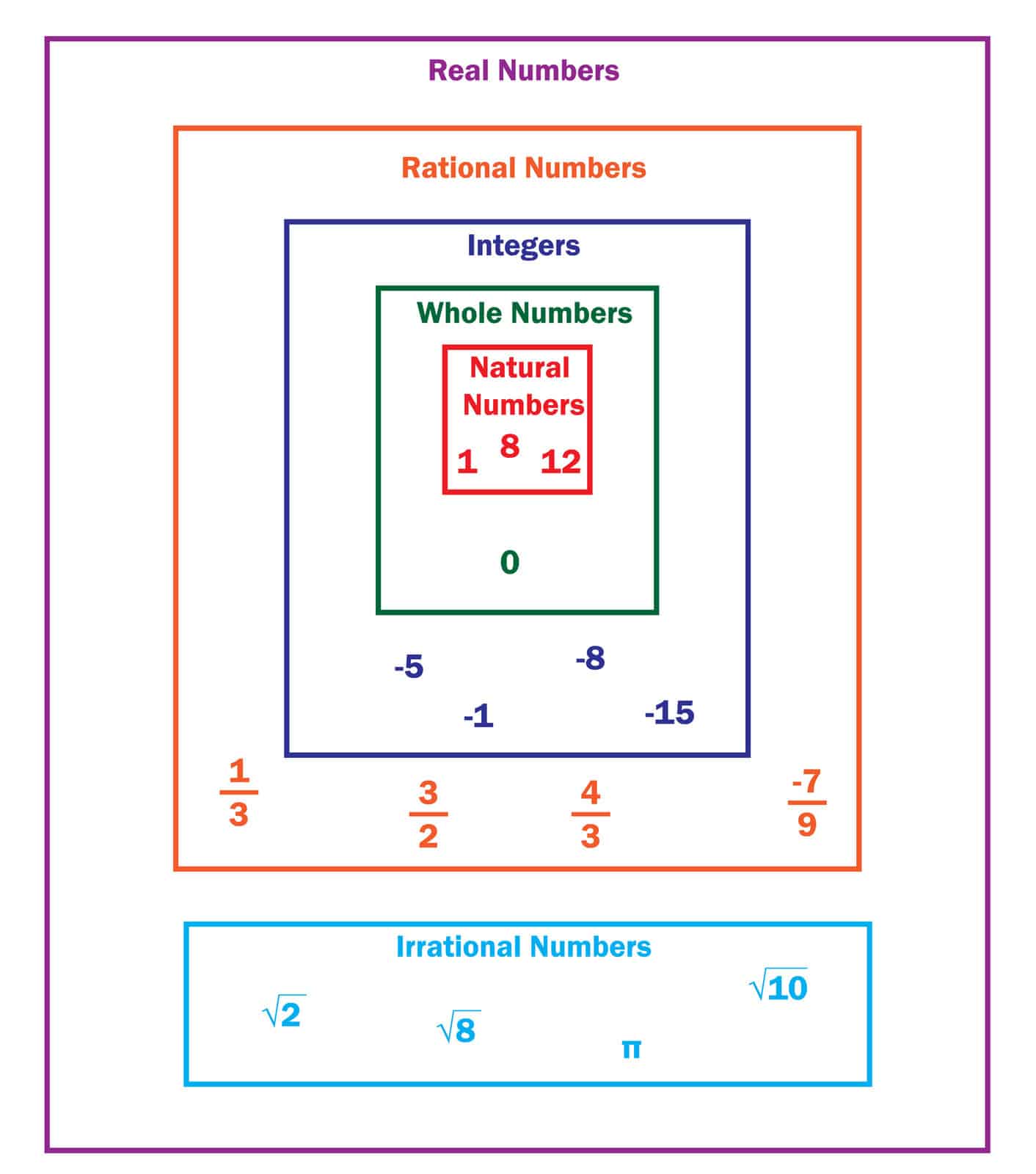
As we know from before, there are many sets of numbers like N stands for natural numbers {0, 1, 2, 3,}. Z stands for integer numbers {…, -2, -1, 0, 1, 2, 3,}. and stands for rational numbers and IR irrational numbers.
So, what are rational numbers in mathematics? Each time we need to know more about numbers and how we can use them to solve the problems facing us in our life,
The Definition of a Rational Number
A rational number is any number that can be written as a fraction using two integers, every integer is a rational number. which can be expressed as the quotient or fraction p/q of two integers, a numerator p, and a non-zero denominator q. For example, -3/7 is a rational number.
Two different fractions may correspond to the same rational number. Every whole number is a Rational Number. The field of rational numbers is usually denoted by a boldface Q.
Note that while ratios can always be expressed as fractions, they can appear in different ways, too such as, 7/8, 3 /62, 2.5, 4%. A rational number is a number you can write as a fraction, as ½, ¼, 2/3… All are rational numbers -3/7 is a rational number, let us ask if 2 is a rational number?
Yes, 2 sometimes is a number that can be more in different ways. We can write 2 as the same 2/1or 4/8. It’s also a whole number and an integer number. Any number can be written as a fraction, with a numerator and a denominator to traduce it is a rational number. Now, what if we said 0.23 is a rational number?
Remember what we said about writing a number as a fraction, this will be a rational number. So, 0.23 can be written as 23/100 which is a rational number and 3/4 = 75/100 = 0.75.0.5 is a fraction ½, all decimals. So, decimals are rational numbers.
Rational Numbers on a Number Line
Rational Numbers on a Number Line We want to understand a lot about rational numbers and how we can represent them on a number line. We will learn how we can do this. Note: The point O represents the integer 0.
Thus, we may represent any integer by a point on the number line. Every positive integer lies on the right of O and every negative integer lies on the left of O.
We can represent rational numbers on the number line in the same way. As we have learned to represent integers on the number line.
To represent rational numbers on the number line, first, we need to draw a straight line and mark a point O on it to represent the rational number zero. The positive (+ve) rational numbers will be represented by points on the number line lying on the right side of O and negative (-ve) rational numbers.
If we mark a point A on the line to the right of O to represent 1, then OA = 1 unit. Similarly, if we choose a point A’ on the line to the left of O to represent -1, then OA’ = 1 unit.
Now we try to Consider the following examples on the representation of rational numbers on the number line;
1. Represent 1/2 and −1/2on the number line.
Solution:
Draw a line. Take a point O on it. Let the point O represent 0. Set off unit lengths OA to the right side of O and OA’ to the left side of O.
Then, A represents integer 1 and A’ represents the integer -1.
Divide the segment OA into two equal parts. Let P be the mid-point of segment OA and OP be the first part out of these two parts. Thus, OP = PA = 1/2. Since O represents 0 and A represents 1, therefore P represents the rational number 1/2.
Again, divide OA’ into two equal parts using the ruler. Let OP be the first part out of these two parts. Thus, OP’ = PA’ = −1/2. Since O represents 0 and A’ represents -1, therefore P’ represents the rational number −1/2.
2. Represent 2/3 and −2/3on the number line.
Solution:
Draw a line. Take a point O on it. Let it represent 0. From the point, O set off unit distances OA to the right side of O and OA’ to the left side of O, respectively.
Divide OA into three equal parts using the ruler. Let OP be the segment showing 2 parts out of 3. Then the point P represents the rational number 2/3.
Again, divide OA’ into three equal parts. Let OP’ be the segment consisting of 2 parts out of these 3 parts. Then, the point P’ represents the rational number −2/3.
3. Represent 13/5 and −13/5on the number line.
Solution: Draw a line. Take a point O on it. Let it represent 0.
Now, 13/5 = 2 3/5 = 2 + 3/5
From O, set off unit distances OA, AB, and BC to the right of O., the points A, B, and C represent the integers 1, 2, and 3 respectively.
Represent 13/5 and −13/5on the number line. Now, take 2 units OA and AB, and divide the third unit BC into 5 equal parts using the ruler. Take 3 parts out of these 5 parts to reach a point P. Then point P represents the rational number 13/5.
Again, from the point O, set off unit distances to the left. Let these segments be OA’, A’ B’, B’ C’, etc. Then, the points A’, B’, and C’ represent the integers -1, -2, -3 respectively.
Now, = -13/5 = -(2 + 3/5)
Take 2 full unit lengths to the left of O. Divide the third unit B’ C’ into 5 equal parts using the ruler. Take 3 parts out of these 5 parts to reach a point P’. Then, the point P’ represents the rational number -13/5.
Thus, we can represent every rational number by a point on the number line. Note that:
According to the real numbers system, the basic real number is one, the real number system is all the numbers’ types on the number line.
We will learn how to find the rational number in different forms using the properties in expressing a given rational number.
1. Express −3/10 as a rational number with denominator 20.
Solution:
To express −3/10as a rational number with denominator 20, we first find the number which when multiplied by 10 gives 20.
Clearly, such a number = 20 ÷ 10 = 2
Multiplying the numerator and denominator of −3/10time 2, we have
−3/10= (−3) ×2/10×2 = −6/20Therefore, expressing −3/10as a rational number with denominator 20 is −6/20.
2. Express −7/10as a rational number with denominator -30.
Solution:
To express −7/10 as a rational number with denominator -30, we first
find a number which when multiplied by 10 gives -30.
Clearly, such a number is = (-30) ÷ 10 = -3.
Multiplying the numerator and denominator of −3/10−310 by -3, we have
−7/10= (−7) × (−3) /10× (−3) = 21/−30
Therefore, expressing −7/10as a rational number with denominator -30 is 21/−30.
3. Express 42/−63 as a rational number with denominator 3.
Solution:
To express 42/−63 as a rational number with denominator 3, we first find a number that gives 3 when -63 is divided by it.
Clearly, such a number = (-63) ÷ 3 = -21
Dividing the numerator and denominator of 42/-63 by -21, we get
42/−63 = 42÷ (−21)/ (−63) ÷ (−21) = −2/3
Therefore, expressing 42/−63 as a rational number in different forms with denominator 3 is −2/3.
4. Fill in the blanks with the appropriate number in the denominator:
7/13 = 35/….= −63/….
Solution:
We have, 35 ÷ 7 = 5
Therefore, 7/13 = 7×5/13×5 = 35/65
Similarly, we have (-63) ÷ 7 = -9
Therefore, 7/13 = 7× (−9)/13× (-9) = −63/-117
Hence, 7/13 = 35/65 = −63/117
We will learn now about the equality of rational numbers with common denominators.
How to determine whether the two given rational numbers are equal or not with the common denominator?
We know there are many methods to determine the equality of two rational numbers, but here we will learn the method of equality of two rational numbers with the same denominator.
In this method, denominators of the given rational numbers are made equal by using the following steps:
Step 1: Obtain the two numbers.
Step 2: Multiply the numerator and denominator of the first number by the denominator of the second number.
Step 3: Multiply the numerator and denominator of the second number by the denominator of the first number.
Step4: Check the numerators of the two numbers obtained in steps 2 and 3. If their numerators are equal, then the given rational numbers are equal, otherwise, they are not equal.
Solved examples:
1. Are the rational numbers −9/12and 21/−28equal?
Solution:
Multiplying the numerator and denominator of −9/12by the denominator of 21/−28 i.e. by -28, we get −9/12= (−9) × (−28)/12× (−28) = 252/−336
Multiplying the numerator and denominator of 21/−28by the denominator of −9/12i.e., by 12, we get 21/−28= 21×12/ (−28) ×12= 252/−336
The numerators of the above obtained rational numbers are equal.
Therefore, the given rational numbers −9/12and 21/−28are equal.
2. Show that the rational numbers −6/8and 10/−15are not equal.
Solution:
Multiplying the numerator and denominator of −6/8by the denominator of 10/−15i.e. -15,
We get −6/8 = (−6) × (−15)/8× (−15) = 90/−120
Multiplying the numerator and denominator of 10/−15by the denominator of −6/8i.e. 8,
We get 10/−15 = 10×8/ (−15) ×8= 80/−120
We find that the numerators of rational numbers 90/−120and 80/−120are unequal.
Therefore, the given rational numbers −6/8and 10/−15 are unequal.
How to determine whether the two given rational numbers are equal or not using a standard form?
We know there are many methods to determine the equality of two rational numbers but here we will learn the method of equality of two rational numbers using a standard form.
To determine the equality of two rational numbers, we express both the rational numbers in the standard form. If they have the same standard form, they are equal, otherwise, they are not equal.
Solved examples on equality of rational numbers using the standard form:
1. Are the rational numbers 14/−35and −26/65equal?
Solution:
First, we express the given rational numbers in the standard form.
14/−35
The denominator of 14/−35is negative. So, we first make it positive.
Multiplying the numerator and denominator of 14/−35by -1, we get
= 14× (−1)/ (−35) × (−1) ⇒ 14/−35= −14/35 Standard form
The greatest common divisor of 14 and 35 is 7.
Dividing the numerator and denominator by the greatest common divisor of 14 and 35 i.e. 7, we get⇒ 14/−35= (−14) ÷7/35÷7⇒ −2/5
And, −26/65is already in the standard form.
The greatest common divisor of 26 and 65 is 13.
Dividing the numerator and denominator by the greatest common divisor of 26 and 65 i.e., 13
⇒ −26/65= (−26) ÷13/65÷13
⇒ −26/65= −2/3
The given rational numbers have the same standard form.
Hence, 14/−35= −26/65
Therefore, the given rational numbers 14/−35and −26/65are equal.
2. Are the rational numbers −12/40and 24/−54equal?
Solution:
To test the equality of the given rational numbers, we first express them in the standard form. −12/40 is already in the standard form.
The greatest common divisor of 12 and 40 is 4.
Dividing the numerator and denominator by the greatest common divisor of 12 and 40 i.e. 4, we get −12/40= (−12) ÷4/40÷4⇒ −12/40= −3/10
And 24/−54is not in standard form so, we first express them in the standard form.
The denominator of 24/−54 is negative. So, we first make it positive.
24/-54 =24(-1) / (-54) (-1) =-24/54
The greatest common divisor of 24 and 54 is 6.
Dividing the numerator and denominator by the greatest common divisor of -24 and 54 i.e. 6, we get, -24 ÷6/54 ÷6 ⇒ -4/9
The given rational numbers have different standard forms.
-3/10 ≠ -4/9
Therefore, the given rational numbers -3/10 and -4/9
Are not equal.
We will learn about the equality of rational numbers using cross multiplication.
We know there are many methods to determine the equality of two rational numbers but here we will learn the method of equality of two rational numbers using cross multiplication.
In this method, to determine the equality of two rational numbers a/b and c / d, we use the following result:
a / b = c / d⇔ a × d = b × c
⇔ The numerator of first × Denominator of second = Denominator of first × Numerator of a second.
Solved examples on equality of rational numbers using cross multiplication:
1. Which of the following pairs of rational numbers are equal?
(i) −8/32and 6/−24 (ii) −4/−18and 8/24
Solution:
(i) The given rational numbers are −8/32and 6/−24
Numerator of first × Denominator of second = (-8) × (-24) = 192 and, Denominator of first × Numerator of second = 32 × 6 = 192.
Clearly,
The numerator of first × Denominator of second = Denominator of first × Numerator of second
Hence, −8/32= 6/−24
Therefore, the given rational numbers −8/32 and 6/−24 are equal.
(ii) The given rational numbers are −4/−18and 8/24
The numerator of first × Denominator of second = -4 × 24 = -96 and, Denominator of first × Numerator of second
= (-18) × 8 = -144
Clearly,
The numerator of first × Denominator of the second ≠ Denominator of first × Numerator of second
Hence, −4/−18≠ 8/24.
Therefore, the given rational numbers −4/−18and 8/24 are not equal.
2. If −6/8= k/64, find the value of k.
Solution:
We know that a/b = c /d if ad = b c
Therefore, −6/8= k/64⇒ -6 × 64 = 8 × k,
[Numerator of first × Denominator of second = Denominator of first × Numerator of second]
⇒ -384 = 8k
⇒ 8k = -384
⇒ 8k/8 = −384/8, [Dividing both sides by 8]
⇒ k = -48
Therefore, the value of k = -48
3. If 7/m = 49/63, find the value of m.
Solution:
To write 49/63 as a rational number with numerator 7, we first find a number which when divided 49 gives 7.
Such a number is 49 ÷ 7 = 7.
Dividing the numerator and denominator of 49/63 by 7, we have
49/63 = 49÷7/63÷7 = 7/9
Therefore, 7/m = 49/63
⇒ 7/m = 7/9
⇒ m = 9
4. Fill in the blank: −7/15=…. /135
Solution:
To fill the required blank, we have to express -7 as a rational number with denominator 135. For this, we first find an integer that when multiplied with 15 gives us 135.
Such an integer is 135 ÷ 15 = 9
Multiplying the numerator and denominator of −7/15by 9, we get
−7/15= (−7) ×9/15×9= −63/135
Therefore, the required number is -63.
Arithmetic Operations on Rational Numbers
Rational numbers can be added, subtracted, multiplied, or divided just like fractions, decimals,
Addition of rational numbers, Rational numbers subtraction, Rational Numbers multiplication, Division of rational numbers.
Properties of Addition of Rational Numbers
We will learn the properties of addition of rational numbers i.e. closure property, commutative property, and associative property, the existence of additive identity property, and the existence of additive inverse property of addition of rational numbers.
(1) Closure property: of addition of rational numbers,
The sum of two rational numbers is always a rational number.
If a/b and c/d are any two rational numbers, then (a/b + c/d) is also a rational number.
For example:
Consider the rational numbers 1/3 and 3/4,
(1/3 + 3/4) = (4 + 9)/12= 13/12, is a rational number
Consider the rational numbers -5/12 and -1/4 Then,
(-5/12 + -1/4) = {-5 + (-3)}/12= -8/12 = -2/3, is a rational number
Consider the rational numbers -2/3 and 4/5 then,
(-2/3 + 4/5) = (-10 + 12)/15 = 2/15, is a rational number
(2) Commutative property of addition of rational numbers:
Two rational numbers can be added in any order.
Thus, for any two rational numbers a/b and c/d, we have
(a/b + c/d) = (c/d + a/b)
For example:
(i) (1/2 + 3/4) = (2 + 3) /4=5/4 and (3/4 + 1/2) = (3 + 2) /4= 5/4
Therefore, (1/2 + 3/4) = (3/4 + 1/2)
(ii) (3/8 + -5/6) = {9 + (-20)}/24 = -11/24 and (-5/6 + 3/8)
= {-20 + 9} /24= -11/24
Therefore, (3/8 + -5/6) = (-5/6 + 3/8)
(iii) (-1/2 + -2/3) = {(-3) + (-4)} /6 = -7/6
and (-2/3 + -1/2) = {(-4) + (-3)}/6= -7/6
Therefore, (-1/2 + -2/3) = (-2/3 + -1/2)
(3) Associative property of addition of rational numbers:
While adding three rational numbers, they can be grouped in any order.
Thus, for any three rational numbers a/b, c /d and e/f, we have
(a/b + c/d) + e/f = a/b + (c/d + e/f)
For example:
Consider three rationales -2/3, 5/7 and 1/6 Then,
{(-2/3 + 5/7) + 1/6} = {(-14 + 15) /21 + 1/6} = (1/21 + 1/6) = (2 + 7) /42
= 9/42 = 3/14
and {(-2/3 + (5/7 + 1/6)} = {-2/3 + (30 + 7)/42} = (-2/3 + 37/42)
= (-28 + 37) /42 = 9/42 = 3/14
Therefore, {(-2/3 + 5/7) + 1/6} = {-2/3 + (5/7 + 1/6)}
(4) Existence of additive identity property of addition of rational numbers:
0 is a rational number such that the sum of any rational number and 0 is the rational number itself.
Thus, (a/b + 0) = (0 + a/b) = a/b, for every rational number a/b
0 is called the additive identity for rationales.
For example:
(i) (3/5 + 0) = (3/5 + 0/5) = (3 + 0)/5 = 3/5 and similarly, (0 + 3/5) = 3/5
Therefore, (3/5 + 0) = (0 + 3/5) = 3/5
(ii) (-2/3 + 0) = (-2/3 + 0/3) = (-2 + 0)/3 = -2/3 and similarly, (0 + -2/3)
= -2/3 Therefore, (-2/3 + 0) = (0 + -2/3) = -2/3
(5) Existence of additive inverse property of addition of rational numbers:
For every rational number a/b, there exists a rational number –a/b
such that (a/b + -a/b) = {a + (-a)}/b = 0/b = 0 and similarly, (-a/b + a/b) = 0.
Thus, (a/b + -a/b) = (-a/b + a/b) = 0.
-a/b is called the additive inverse of a/b
For example:
(4/7 + -4/7) = {4 + (-4)}/7 = 0/7 = 0 and similarly, (-4/7 + 4/7) = 0
Thus, 4/7 and -4/7 are additive inverses of each other.
Example:
(2/5 + -2/5) = {2 + (-2)}/5 = 0/5 = 0 and similarly, (-2/5 + 2/5) = 0
Thus, 2/5 and -2/5 are additive inverses of each other.
Adding and subtracting rational numbers
The process of adding and subtracting rational numbers can be done in the same way as fractions. To add or subtract any two rational numbers, we make their denominators the same and then add the numerators.
The questions are based on adding and subtracting rational numbers with the same denominators and adding and subtracting rational numbers with different denominators.
When Given Numbers have same Denominator:
In this case, we define (a/b + c/b) = (a + c) / b
For example: Add 3/7 and 23/7
Solution:
3/7 + 23/7= (3 + 23)/7= 26/7, [Since, 3 + 23 = 26]
Therefore, 3/7 + 23/7 = 26/7
Example: Add 8/13 and -5/13
Solution:
3/13 + -5/13= [3 + (-5)]/13= (3 -5)/13= -2/13, [Since, 3 – 5 = -2]
Therefore, 3/13 + -5/13 = = -2/13.
Now try to solve first by yourself. Add the following rational numbers:
-5/7 and 3/7 is has the same denominator? Yes 7
= (-5) /7 + 3/7 = (-5+3) /7= -2/7
-15/4 and 7/4 is has the same denominator? Yes 4
= (-15) +7/4 = -8/4 =-2
-8/11 and -4/11 is having the same denominator? Yes 11
= (-8+-4) /11=-12/11
6/13 and -9/13 is having the same denominator? Yes 13
= (6+ – 9) /13=-3/6= -1/2
We will learn now the addition of rational number with different denominator.
To find the sum of two rational numbers which do not have the same denominator, we follow the following steps:
Step 1: Let us obtain the rational numbers and see whether their denominators are positive or not. If the denominator of one (or both) of the numerators is negative, re-arrange
It is so that the denominators become positive.
Step 2: Find the lowest common multiple of the denominators of the two given rational numbers.
Step3: Express both the rational numbers in step I so that the lowest common multiple of the denominators becomes their common denominator.
Step 4: Write a rational number whose numerator is equal to the sum of the numerators of rational numbers obtained in step 3 and denominators are the lowest common multiple obtained in step 2.
Step 5: The rational number obtained in step 4 is the required sum (simplify if required).
It means when Denominators of Given Numbers are Unequal:
In this case, we take the (least common multiple) LCM of their denominators and express each of the given numbers with this LCM as the common denominator. Now, we add these numbers.
For example:
1. Add 5/6 and 7/9
Solution:
The denominators of the given numerators are positive.
The LCM of the denominators 6 and 9 is 18.
Now, we express 5/6 and 7/9 into forms in which both of them have the same denominator 18.
We have, 5/6 = 5 × 3/6 × 3 = 15/18, and 7/9 = 7 × 2/9 × 2 = 14/18,
Therefore, 5/6 + 7/9 = 15/18 + 14/18 = (15 + 14)/18= 29/18
Example: 2. Add the following rational numbers:
3/4 and -3/5 are having the same denominator? No 4, 5 The
LCM of the denominators 4and 5 is 20. Now, we express
3/4 and -3/5 into forms in, which both of them have the
Same denominator 20.
By multiply first 3/4 by 5/5, and the
Second-3/5 by 4/4 to be 20.
= (¾ ×5/5) + (-3/5×4/4) = 15/20 + (-12/20) =3/20
Example: 3. Add: 5/6 and -3/7
Solution:
The denominators of the given rational numbers are 6 and 7 respectively.
The LCM of 6 and 7 is 42.
Now, we rewrite the given rational numbers into forms in which both of them have the same denominator.
5/6 = 5 × 7/6 × 7 = 35/42, and-3/7 = -3 × 6/7 × 6 = -18/42,
Therefore, 5/6 + -3/7= 35/42 + -18/42= (35 – 18)/42=17/42
Example: 4. Find the sum: -9/16 + 5/12
Solution:
LCM of 16 and 12 = (4 × 4 × 3) = 48.
Therefore, -9/16 + 5/12= 3 × (-9) + 4 × 5/48= (-27) + 20/48
= -7/48
Example: 5. Add:
-7/27 and 11/9 can you tell us the stapes we do to solve?
=-7/27 + (11×3/9×3) = -7/27+ 33/27= -26/27
Example: 6. Add: 13/-4 and -5/8
Now you try to explain how you solve this one by yourself as we did before.
= (13×…. /-4×….) +-5/8=….
Example: 7. Add: 4/7 and 5
Solution:
We have, 5 = 5/1
Denominators of the two rational numbers are positive. We now re-write them so that they have a common denominator equal to the LCM of the denominators.
In this case, the denominators are 7 and 1.
The LCM of 7 and 1 is 7.
We have, 5 = 5/1 = 5×7/1×7= 35/7 Therefore, 4/7 + 5= 4/7 + 5/1
= 4/7 + 35/7= 4+35/7= 39/7
Example: 8. Add: -3 and 3/5
We rewrite the first number -3/1 in this case the denominators are 1and 5, The LCM of 5 and 1 is 5.
= (-3/1) + 3/5= (-3×5/1×5) +3/5 = -15/5+3/5 = -12/5
Example: 9. Simplify: 7/-12+ 5/−4
Solution:
First, we write each of the given numbers with positive denominator.
7/−12= 7× (−1)/ (−12) × (−1) = −7/12, [Multiplying the numerator and denominator by -1]
⇒ 7/−12 = −7/12
5/−4 = 5× (−1)/ (−4) × (−1) = −5/4, [Multiplying the numerator and denominator by -1]
⇒ 5/-4 = −5/4
Therefore, 7/-12 + 5/−4 = −7/12+ −5/4
Now, we find the LCM of 12 and 4. The LCM of 12 and 4 = 12
Rewriting −5/4in the form in which it has denominator 12, we get
−5/4= (−5) ×3/4×3= −15/12
Therefore, 7/-12 + 5/−4
= −7/12+ −5/4= −7/12+ −15/12
= ((−7) + (−15) /12= −22/12= −11/6
Thus, 7/−12+ 5/−4= −11/6
Example: 10. Add: 5/6 and 7/9
Solution:
The denominators of the given numerators are positive.
The LCM of the denominators 6 and 9 is 18.
Now, we express 5/6 and 7/9 into forms in which both of them have the same denominator 18.
We have,
5/6 = 5 × 3/6 × 3 = 15/18
And
7/9 = 7 × 2/9 × 2 = 14/18
Therefore, 5/6 + 7/9
= 15/18 + 14/18
= (15 + 14) /18
= 29/18
Example: 11. Find the sum: -9/16 + 5/12
Solution:
LCM of 16 and 12 = (4 × 4 × 3) = 48.
Therefore, -9/16 + 5/12= 3 × (-9) + 4 × 5/48= (-27) + 20/48= -7/48
We will learn about the subtraction of rational numbers. If a/b and c /d are two rational numbers, then subtracting c /d from a/b means adding additive inverse (negative) of c /d to a/b. The subtracting of c / d from a/b is written as a/b – c /d.
Thus, we have
a /b – c/d = a/b + (-c/d), [Since additive inverse of c/d is -c/d]
We will learn the subtraction of rational numbers with the same denominator. To subtract two rational numbers having the same denominator, we follow the following steps:
Step 1: Let us obtain the numerators of two given rational numbers and their common denominator.
Step2: Subtract the first numerator from the second numerator.
Step 3: Write a rational number whose numerator is the difference of two given rational numbers obtained in step 2 and retain the common denominator (simplify if required).
From the above follows steps we conclude that if a/b and c/b are two rational numbers with the same denominator, then a/b – c/b = a – c/b.
1. Find the difference of 5/7 from 13/7
Solution:
13/7 – 5/7= 13 – 5/7= 8/9
Therefore, 13/7 – 5/7 = 8/9.
2. Find the difference of 3/-5 – 4/5
Solution:
3/-5 – 4/5
We first express 3/-5 as a rational number with a positive denominator.
We have, 3/-5 = 3 × (-1)/ (-5) × (-1) = -3/5
Now, 3/-5 – 4/5= (-3/5 – 4/5) = -3 – 4/5= -7/5
Therefore, 3/-5 – 4/5 = -7/5.
3. Subtract -8/11 – 4/11
Solution:
-8/11 – 4/11= -8 – 4/11= -12/11
Therefore, -8/11 – 4/11 = -12/11.
4. Subtract 6/17 from 2/-17
Solution:
We first express 2/-17 as a rational number with positive denominator.
We have, 2/-17 = 2 × (-1) / (-17) × (-1) = -2/17
Now, 2/-17 – 6/17
= -2/17 – 6/17= -2 – 6/17= -8/17
Therefore, 2/-17 – 6/17 = -8/17.
5. Subtract the first rational number from the second rational number: 5/6, 17/6
Solution:
17/6 – 5/6= 17 – 5/6= 12/6= 2
Therefore, 17/6 – 5/6 = 2.
6. Subtract the first rational number from the second rational number: -3/8, -11/8
Solution:
-11/8 – (-3) /8= -11 – (-3) /8= -11 + 3/8= -8/8= -1
Therefore, -11/8 – (-3)/8 = -1
We will learn the subtraction of rational numbers with different denominators. To find the difference between two rational numbers which do not have the same denominator, we follow the following steps:
Step 1: Let us obtain the rational numbers and see whether their denominators are positive or not. If the denominator of one (or both) of the numerators is negative, re-arrange it so that the denominators become positive.
Step2: Find the lowest common multiple of the denominators of the two given rational numbers.
Step 3: Express both the rational numbers in step I so that the lowest common multiple of the denominators becomes their common denominator.
Step 4: Write a rational number whose numerator is equal to the difference of the numerators of rational numbers obtained in step IV and denominators are the lowest common multiple obtained in step 2.
Step 5: The rational number obtained in step 4 is the required difference (simplify if required).
Following examples,
1. Subtract 9 from 4/5
Solution:
We have, 9 = 9/1
Denominators of the two rational numbers are positive. We now re-write them so that they have a common denominator equal to the LCM of the denominators.
In this case, the denominators are 1 and 5.
The LCM of 1 and 5 is 5.
We have, 9 = 9/1 = 9 × 5/1 × 5 = 45/5
Therefore, 4/5 – 9= 4/5 – 9/1= 4/5 – 45/5= (4 – 45)/5= -41/5
Therefore, 4/5 – 9 = -41/5
2. Find the difference of: -3/4 – 5/6
Solution:
The denominators of the given rational numbers are 4 and 6 respectively.
LCM of 4 and 6 = (2 × 2 × 3) = 12.
Now, -3/4 = (-3) × 3/4 × 3 = -9/12, and 5/6 = 5 × 2/6 × 2 = 10/12
Therefore, -3/4 – 5/6= -9/12 – 10/12= (-9 – 10)/12= -19/12
Therefore, -3/4 – 5/6 = -19/12
3. Simplify: 3/-15 – 7/-12
Solution:
First, we write each of the given numbers with positive denominator.
3/-15 = 3 × (-1) / (-15) × (-1) = -3/15,
[Multiplying the numerator and denominator by -1]
⇒ 3/-15 = -3/15
7/-12 = 7 × (-1) / (-12) × (-1) = -7/12,
[Multiplying the numerator and denominator by -1]
⇒ 7/-12 = -7/12
Therefore, 3/-15 – 7/-12 = -3/15 – (-7)/12
Now, we find the LCM of 15 and 12.
The LCM of 15 and 12 = 60
Rewriting -3/15 in the form in which it has denominator 60, we get
-3/15 = -3 × 4/15 × 4 = -12/60
Rewriting -7/12 in the form in which it has denominator 60, we get
-7/12 = -7 × 5/12 × 5 = -35/60
Therefore, 3/-15 – 7/-12= -3/15 – (-7)/12= -12/60 – (-35)/60
= (-12) – (-35) /60= -12 + 35/60= 23/60
Thus, 3/-15 – 7/-12 = 23/60.
4. Simplify: 11/-18 – 5/12
Solution:
First, we write each one of the given rational numbers with a positive denominator.
The denominator of 5/12 is positive.
The denominator of 11/-18 is negative.
The rational number 11/-18 with a positive denominator is -11/18.
Therefore, 11/-18 – 5/12 = -11/18 – 5/12
The LCM of 18 and 12 is 36.
Rewriting -11/18 in forms having the same denominator 36, we get
-11/18 = (-11) × 2/18 × 2,
[Multiplying the numerator and denominator by 2]
⇒ -11/18 = -22/36
Rewriting 5/12 in forms having the same denominator 66, we get
5/12 = 5 × 3/12 × 3,
[Multiplying the numerator and denominator by 3]
⇒ 5/12 = 15/36
Therefore, 11/-18 – 5/12= -11/18 – 5/12= -22/36 – 15/36
= -22 – 15/36= -37/36
Therefore, 11/-18 – 5/12 = -37/36
5. Subtract 2/5 from 4/7
Solution:
The additive inverse of 2/5 is -2/5
Therefore, 4/7 – 2/5 = 4/7 + (-2/5)
⇒ 4/7 – 2/5 = 4 × 5/7 × 5 + (-2) × 7/5 × 7
= 20/35 + -14/35= 20 + (-14) /35= 6/35
Therefore, 4/7 – 2/5 = 6/35
6. Subtract -6/7 from -5/8.
Solution:
The additive inverse of -6/7 is 6/7
Therefore, -5/8 – (-6/7) = -5/8 + 6/7, [Since, – (-6/7) = 6/7)]
⇒ -5/8 – (-6/7) = -5 × 7/8 × 7 + 6 × 8/7 × 8⇒ -5/8 – (-6/7) = -35/56 + 48/56
⇒ -5/8 – (-6/7) = -35 + 48/56⇒ -5/8 – (-6/7) = 13/56
Therefore, -5/8 – (-6/7) = 13/56
7. Subtract -4/9 from 2/5
Solution:
The additive inverse of -4/9 is 4/9.
Therefore, 2/5 – (-4/9) = 2/5 + 4/9, [Since, – (-4/9) = 4/9)]
⇒ 2/5 – (-4/9) = 2 × 9/5 × 9 + 4 × 5/9 × 5
⇒ 2/5 – (-4/9) = 18/45 + 20/45
⇒ 2/5 – (-4/9) = 18 + 20/45
Therefore, 2/5 – (-4/9) = 38/45
8. The sum of two rational numbers is -3/5. If one of the numbers
Is -9/20, find the other.
Solution:
Sum other number = -3/5, One number = -9/20
Therefore, the other number = Sum of the two rational numbers – One of the given rational numbers.
= -3/5 – (-9/20)
= -3/5 + 9/20, [Since – (-9/20) = 9/20]
= (-3) × 4 + 9 × 1/20= -12 + 9/20= -3/20
Therefore, the required rational number is -3/20.
9. Which rational number should be added to -7/11 to get 4/7?
Solution:
Sum of the given number and the required rational number = 4/7.
Given rational number = -7/11.
Therefore, the required number = Sum – Given number
= 4/7 + 7/11= 4 × 11/ 7 ×11 + 7 × 7/11 × 7
= 44/77 + 49/77= 44 + 49/ 77= 93/77
Thus, the rational number 93/77 should be added to -7/11 to get 4/7.
10. What should be subtracted from -4/5 to get 6/15?
Solution:
Difference between the given rational number and the required rational number = 6/15.
Given rational number = -4/5.
Therefore, the required rational number = -4/5 – 6/15
= -4/5 + -6/15= (-4) × 3/5 × 3 + -6/15= -12/15 + -6/15
= (-12) + (-6) /15= -18/15= -6/5
Thus, the rational number -6/5 was subtracted from -4/5 to get 6/15.
The process of multiplying and dividing rational numbers can be done in the same way as fractions. To multiply any two rational numbers, we multiply their numerators and their denominators separately and simplify the resultant fraction.
That means when we multiply two rational numbers a / b and c / d:
a / b × c / d = a × c / b × d = a c / b d
Example: 3/5 × -2/7 = (3 × -2)/ (5 × 7) = -6/35
Example: Find the product of -5 / 7 and 9.
-5 / 7 × 9 = -5 / 7 × 9 / 1 = -5 × 9 /7 × 1 = -45 / 7
Example: Find product of 1 / 2 and -3 / 4,
1 / 2 × -3 / 4 = 1 × (-3) / 2 × 4 = -3 / 8
(Closure property)
Example: -3 / 4 × 5 / 7 = -3 × 5 / 4 × 7 = -15 / 28
Example find the product:
Solution:
Examples multiply:
Solution:
= 40 / 400
Dividing both the numerator and denominator by the greatest common divisor of 40 and 400 which is 40.
= 40 ÷ 40 / 400 ÷ 40 = 1 / 10
= 9 × 22 / -11 × -27 = 198 / 297 =198 ÷ 99 / 297÷ 99 = 2 / 3
Example Simplify:
[-2 / 3 × 9 / 5] + [2 / 3 × -6 / 7]
Solution:
We have, [-2 / 3 × 9 / 5] + [2 / 3 × -6 / 7] = -18 / 15 + [-12 / 21]
= -18 × 7 + (-12 × 5) / 105= -126 + (-60) / 105 = -126 – 60 / 105
-186 / 105 = -62 / 35
Example multiply 2/3 and 5/7.
Solution:
= (2/3) × (5/7) Multiply the numerators and denominators
. = (2×5) / (3 × 7) = 10/21
Example: Evaluate:
(4/-11) × (-22/8)
Solution: = (4/-11) × (-22/8)
Before we multiply numerators and denominators, we can simplify as shown below.
4/-11 × -22 / 8 = 1 / 1 × -2 / 2 = (-2) / (-2) = 1 simplify divided the numerator and the denominator
of first number by 4 and second number by 11.
Example: Multiply 2¼ and 3½.
Solution:
= (21/4) × (31/2) Converting the mixed fractions to improper fractions.
= (9/4) × (7/2) = (9 × 7) / (4 × 2) = 63/8= 7 7/8
To divide any two fractions, we multiply the first fraction (which is dividend) by the reciprocal of the second fraction.
Example: 3/5 ÷ 2/7=3/5 × 7/2 = 21/10.
For example: a) 5/7 × 7/5 = 1 b) -3/ 8 × -8 / 3= 1=
Reciprocal of -1 =1 / -1 = 1
To divide one rational number by other rational numbers we multiply the rational number by
the reciprocal of the other.
a / b ÷ c/d = a / b × reciprocal of c/d = a / b × d / c = ad / bc
For example, 5 / -6 ÷ -3 / +2 = 5 / -6 × reciprocal of [-3 / 2] = 5 / -6 × +2 / -3
= 5 × 2 / -6 × (-3) = 10 / 18 = 5 / 9
For example, 0 ÷ 2 / 5 = 0; 0 ÷ -3 / 8 = 0.
Note:
i.e., a / b ÷ c / d = [a d / b c] is also rational number.
2. Division of any rational number is divided by 1, the quotient is a rational number itself.
3. When a rational number is divided by 1, the quotient is a rational number itself.
For example, 3 / 4 ÷ 1 = 3 / 4.
Division of Rational Numbers Problems with Solutions:
Find the value of the following:
Solution:
So, 3 / 13 ÷ [-4 / 65] = -15 / 4.
d)-2 / 8 ÷ – 2 / 8 = -2 / 8 × 8 / -2 = (-2) × 8 / 8 × (-2) = 1 ×1/ 1 ×1 = 1 so, -2 / 8 ÷ -2 / 8 =1
So, -2 / 8 ÷ -2/ 8 = 1
Remember To divide a rational number ‘a/b’ by another rational number ‘c/d’, multiply the first rational number ‘a/b’ by the multiplicative inverse of the second rational number ‘c/d’.
Multiplicative inverse of ‘c/d’ is /c’.
(a / b) ÷ (c / d) = (a / b) × (d / c) = (a × d) / (b × c)
Note:
In case we have mixed fractions, first, we have to convert them to improper fractions and do the multiplication and division as explained above.
Example: Simplify:
(2/5) ÷ (7/9)
Solution:
= (2 / 5) ÷ (7 / 9) to divide by 7 / 9, multiply by 9 / 7 = (2/5) × (9/7)
Multiply the numerators and denominators.
= (2 × 9) / (5 × 7) = 18 / 35
Example: Simplify:
(-4/9) ÷ (9/-4)
Solution:
= (- 4 / 9) ÷ (9 /-4) to divide by 9 /-4, multiply by -4/9.
= (-4 / 9) × (-4 / 9) multiply the numerators and denominators.
= [(- 4) × (- 4)] / (9 × 9) = 16/81
Example: Simplify: -9 ¾ ÷ 1 ⅞
Solution:
= -9¾ ÷ 1⅞ Converting the mixed numbers to improper fractions
= (-39/4) ÷ (15/8) to divide by 15 / 8, multiply by 8 / 15.
= (-39/4) × (8/15)
Simplify 39 and 15 using 3 times table, 4 and 8 using 4 times table.
= (-13/1) × (2/5) = (-13 × 2) / (1 × 5) = -26 / 5= -5 ⅕
Example:
Mary wants to share three-fourths of a pizza equally with 4 of her friends. How much pizza will each friend get?
Solution:
Amount of pizza each friend will get: = (3 / 4) ÷ 4 = (3 / 4) ÷ (4 / 1)
To divide by 4 / 1, multiply by 1 / 4.
= (3/4) × (1/4) multiply numerators and denominators.
= (3 × 1) / (4 × 4) = 3 /16 each friend will get 3 / 16 of a pizza.
Explore the previous examples and problems, and you will find yourself getting the necessary knowledge and information to fully grasp the concept of rational numbers. So, keep on visiting our LearningMole.
Leave a Reply