10 Interesting Facts about Rational Numbers

Before we start to know about rational numbers, let us remember what we learned from the set of different numbers.

Numbers are the language of mathematics, as they are used to express quantities and they are the basis of mathematics on which arithmetic operations are performed on a daily basis. For example, they are an essential part of money calculation, days, months, or years.

Table of Contents

• Numbers
• Integers and Rational Numbers
• Tips and Tricks
• The Rational Number in Mathematics
• Definition
• Examples
• Types of Rational Numbers
• How to Identify
• Rational Numbers in Decimal Form
• Rational Numbers in Different Forms
• Operations on Rational Numbers
• Comparison between Rational Numbers
• Arrange Rational Numbers in Ascending Order
• Arrange Rational Numbers in Descending Order
• Frequently Asked Questions

Numbers

There are differences in the form of numbers. Their pronunciation and the way they are written in every culture and language differences. Just as every language is different from other languages ​​according to culture. There are Arabic numbers and Indian numbers, but which are the numbers that form the mathematical symbols?

The role of scientists in the discovery and development of numbers greatly contributed. Most notably, was the Muslim scientist Al-Khwarizmi, who discovered the zero by which humans could count to infinity. So, we need to know more about numbers and how we can use them to solve the problems that face us in our lives.

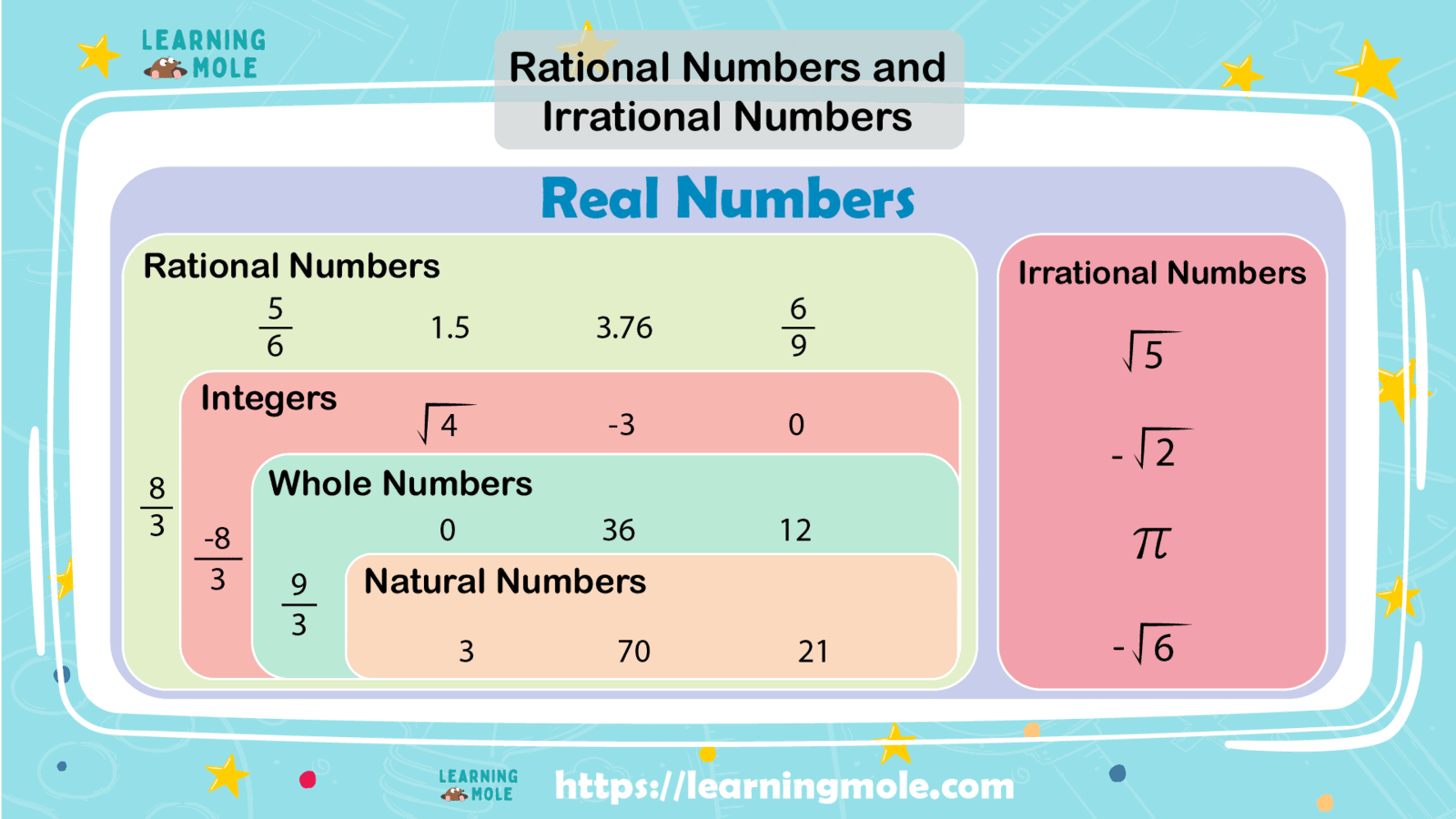
Integers and Rational Numbers

One of the first numbers that scientists discovered were the numbers used for counting, whole numbers {1,2, 3……}, then the natural numbers {0,1,2, 3….}, followed by the integer numbers {…-3, -2, -1,0,1,2, 3…}, and rational numbers.

Rational numbers are one very common type of number that we usually study after integers in math. These numbers are written in the form of p/q, where p and q can be any integer and q ≠ 0. Mostly, people find it confusing to differentiate between fractions and rational numbers because of the basic structure of numbers which is the p/q form.

Fractions are made up of whole numbers while rational numbers are made up of integers as their numerator and denominator. Let’s learn more about rational numbers.

Before we start the introduction of rational numbers let us recall some basic mathematical rules. For two given integers a and b: their sum is a + b, their product is a × b, and their difference is a– b. They are always integers.

However, it may not always be possible for a given integer to be exactly divided by another given integer. This means that the result of the division of an integer by a non-zero integer may or may not be an integer. For example, when 7 is divided by 3, the result is not an integer since we know 7/3 is a fraction.

 Thus, there is a need to extend the system of integers. So, that it may also be possible to divide any given integer by any other given integer that is not zero (because division by zero is not possible).

Now, we shall introduce the system of rational numbers, the comparison of rational numbers, various operations on rational numbers, and the properties of these operations on rational numbers.

Rational Numbers Tips and Tricks

• Rational numbers are NOT only fractions but any number that can be expressed as fraction
• Natural numbers, whole numbers, integers, fractions of integers, and terminating decimals are rational numbers
• Non-terminating decimals with repeating patterns of decimals are also rational numbers
• If a fraction has a negative sign either in the numerator or in the denominator or in front of the fraction, the fraction is negative. i.e., -a/b = a/-b.

The Rational Numbers in Mathematics

Do you know where the word “Rational” originated? It originated from the word “ratio”. So, rational numbers are very well related to the ratio concept of ratio.

Every integer is a rational number. You learned that the positive numbers, the negative numbers, and zero are called real numbers. So, the rational numbers are all real numbers and can be positive or negative.

A number that is not rational is called an irrational number. An irrational number is any number that is not rational. It is a number that cannot be written as a ratio of two integers or cannot be written as a fraction.

π is an irrational number, but we will not explain it now, don’t worry. Most of the numbers that people use in their everyday life are rational. These include fractions, integers, and numbers with finite decimal digits.

The Definition of Rational Numbers

A real number can be expressed as the quotient of two integers that are called rational numbers. A rational number is a number that can be expressed as a fraction or a number that is in the form p/q, where p and q are integers and q is not equal to 0.

The set of rational numbers is denoted by Q. In other words, if a number can be expressed as a fraction where both the numerator and the denominator are integers, the number is a rational number.

Examples of Rational Numbers

Remember that if a number can be expressed as a fraction where both the numerator and the denominator are integers, then the number is a rational number. Each number below is a rational number.

0=0/1    , 7=7/1  , 5 2/3=17/3 , 0.43=43/100, – 4/9=-4 /9

And also: 1/3, -2/5, 0.7 or 7/10, and -0.3 or -3/10.

There are different types of rational numbers. We shouldn’t assume that only fractions with integers are rational numbers.

Types of Rational Numbers

Decimals: 0.5, 0.4, 0.8, etc.

Fractions: 2/5, 1/3, 1/4, etc.

Percentage: 50%, 25%, 30%, etc.

Integers: -3.4, 5, etc.

Fractions whose numerators and denominators are integers like 3/7, -6/5, etc.

Terminating decimals like 0.35, 0.7116, 0.9768, etc. For example, -3/7, ½, 2/1

Non-terminating decimals, which are decimals with repeating patterns after the decimal point such as, 0.333…, 1.151515…,0.666…,0.09090909, etc.

A full understanding of rational numbers for students involves an understanding of rational numbers in all of their interpretations. These interpretations can be named in different ways, but in summary, they can be grouped under the headings or concepts of the quotient, measure, ratio, decimal, and operator. We can take any rational number (fraction). The purpose of this review is to discuss which rational number format students should learn first.

Rational numbers can be represented with three related but different notations: fractions, decimals, and percentages. Each notation can express the multiple interpretations of a rational number.

Remember what we said about when we can write a number as a fraction. This will be a rational number. For example, 0.25 can be written as 25/100 which equals ¼ and that is also a rational number and 3/4 = 75/100 = 0.75, 0.5 =5/10 = ½.

How to Identify a Rational Number?

In each of the above cases, the number can be expressed as a fraction of integers. Hence, each of these numbers is a rational number. To find whether a given number is a rational number or not, we can check whether it matches with any of these conditions:

• We can represent the given number as a fraction of integers
• All whole numbers are rational numbers

Rational Numbers in Decimal Form

Rational numbers can also be expressed in decimal form. Did you know that 1.1 is a rational number? Yes, it is because 1.1 can be written as 1.1= 11/10

Rational Numbers in Different Forms

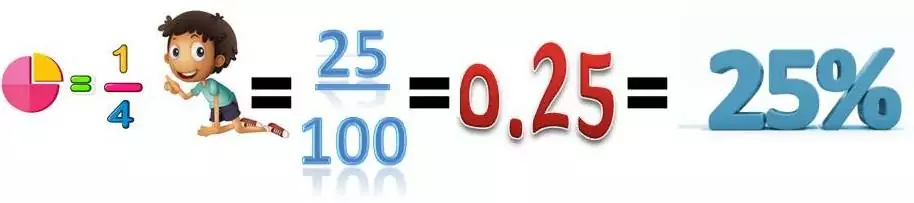
We will learn how to find the rational number in different forms using the properties in expressing a given rational number.

1. Express −3/10as a rational number with denominator 20.

Solution: In order to express −3/10as a rational number with denominator 20, we first find the number which when multiplied by 10 gives 20. Clearly, such a number = 20 ÷ 10 = 2

Multiplying the numerator and denominator of −3/10time 2, we have 

−3/10= (−3) ×2/10×2 = −6/20Therefore, expressing −3/10as a rational number with denominator 20 is −6/20.

• Express −7/10as a rational number with denominator -30.

Solution:  In order to express −7/10 as a rational number with denominator -30, we first find a number that when multiplied by 10 gives -30. Clearly, such a number is = (-30) ÷ 10 = -3.

Multiplying the numerator and denominator of −7/10by -3, we have−7/10= (−7) × (−3)/10 ×(−3)  = 21/−30

Therefore, expressing −7/10as a rational number with denominator -30 is 21/−30.

• Express 42/−63 as a rational number with denominator 3.

Solution:

In order to express 42/−63 as a rational number with denominator 3, we first find a number that gives 3 when -63 is divided by it.

Clearly, such a number = (-63) ÷ 3 = -21

Dividing the numerator and denominator of 42/-63 by -21, we get

42/−63 = 42÷ (−21) / (−63) ÷ (−21) = −2/3

Therefore, expressing 42/−63 as a rational number in different forms with denominator 3 is −2/3.

Operations on Rational Numbers

Addition of Rational Numbers

When the denominators of the given rational numbers are equal:
We add the numerators and keep the denominators the same.

E.g 3/10 + 4/10 = 7/10
When the denominators of given numbers are unequal:
We must use two steps to add two unequal denominators;
-We must find the LCM of the denominator. The LCM of 4 and 5 is 20.
-We must then convert each rational number into the same denominator.

E.g 3/4 + 3/5 = 3×5/20 + 3×4/20
15/20+ 12/20= 27/20

Subtraction of Rational Numbers

When the denominators of the given numbers are equal:
Subtract the numerators and keep the denominator the same.

E.g 4/5 – 2/5 = 2/5

When the denominators of the given numbers are unequal:

We must find the LCM of the denominator. In this example, the LCM of 2 and 3 is 6.

We must convert each fraction into a rational number with the same denominator.

E.g ½ – ⅔ = 1×3/6 – 2×2/6 

4/6 – 3/6 =1/6

Multiplication of Rational Numbers

To multiply two rational numbers, you must multiply the numerator and denominator of the first rational number with the numerator and denominator of the second rational number.

E.g 4/5 x 2/3 = 4×2= 8, 5×3= 15 = 8/15

Division of Rational Numbers

To divide two rational numbers, you must multiply one rational number by the inverted rational number.

E.g 2/3 divided by 1/5= 2/3 X 5/1 (flip the second fraction upside down), then do your steps of multiplication, 2×5=10, 3×1=3 = 10/3

Comparison between Rational Numbers

We will learn now about the comparison between rational numbers. We know how to compare two integers and also two fractions. We know that every positive integer is greater than zero and every negative integer is less than zero.

Also, every positive integer is greater than every negative integer. Similar to the comparison of integers, we have the following facts about how to compare rational numbers, and before you make any comparison between two rational numbers you must remember these facts.

• Every negative rational number is less than 0
• Every positive rational number is greater than every negative rational number
• Every rational number represented by a point on the number line is greater than every rational number represented by points on its left
• Every rational number represented by a point on the number line is less than every rational number represented by paints on its right

How to compare the two rational numbers? In order to compare any two rational numbers, we can use the following:

1: Obtain the given rational numbers

2: Write the given rational numbers so that their denominators are positive

3: Find the LCM of the positive denominators of the rational numbers

4: Express each rational number (obtained in 2) with the LCM (obtained in 3) as a common denominator

5: Compare the numerators of rational numbers obtained in the previous step. The number that has a greater numerator is the greater rational number

Examples:

1. Which of the two rational numbers 1/2 and −2/3is greater?

Solution:

Clearly, 1/2 is a positive rational number, and −2/3is a negative rational number.

We know that every positive rational number is greater than every negative rational number. Therefore, 1/2 > −2/3.

2. Which rational number is greater, 3/−5 or −5/6?

Solution:

We write each of the given numbers with a positive denominator.

First number: 3/-5 = 3× (−1)/ (−5) × (−1) = −3/5

The other number = −5/6.

L.C.M. of 5 and 6 = 30

Therefore, −3/5= (−3) ×6/5×6 = −18/30 and −5/6 = (−5) ×5/6×5 = −25/30

Clearly, -18/30 > −25/30 Hence, 3/-5 > -5/6

3. Which rational number is greater 5/6 or 3/4?

Solution:

Clearly, denominators of the given rational numbers are positive. The denominators are 6 and 4. The LCM of 6 and 4 is 12. So, we first express each rational number with 12 as a common denominator.

Therefore, 5/6 = 5×2/6×2 = 10/12 and 3/4 = 3×3/4×3 = 9/12

We compare the numerators of these rational numbers.

Therefore, 10 > 9⇒ 10/12 > 9/12 ⇒ 5/6 > 3/4.

5. Which rational number is greater −4/5or 5/−7?

Solution:

First, we write each one of the given rational numbers with a positive denominator.

Clearly, the denominator of −4/5 is positive, the denominator of 5/−7 is negative.

So, we express it with a positive denominator as follows:

5/−7= 5× (−1)/ (−7) × (−1) = −5/7, [Multiplying the numerator and denominator time -1]

Now, the LCM of denominators 5and 7 is 35.

We write the rational numbers so that they have a common denominator 35 as follows:

−4/5 = (−4) ×7/5×7 = −28/35 and, −5/7 = (−5) ×5/7×5 = −25/35

Therefore, -25 > -28 ⇒ -25/35 > -28/35 ⇒ −5/7> −4/5 ⇒ 5/-7> −4/5.

For all integers a and b and all positive integers c and d;

1. a/c >b/d if and only if ad >b c.
2. a/c < b/d if and only if ad <b c.

Thus, 4/7 > 3/8 because (4×8) > (3×7).

          7/9 < 4/5 because (7×5) < (4×9).

Arrange the Rational Numbers in Ascending Order

We will learn how to arrange rational numbers in ascending order. The general method is to arrange from the smallest to the largest rational numbers (increasing):

1: Express the given rational numbers with a positive denominator

2: Take the least common multiple (L.C.M.) of this positive denominator

3: Express each rational number (obtained in step 1) with this least common multiple (LCM) as the common denominator

4: The number having the smaller numerator is smaller.       

Examples:

1. Arrange the rational numbers −7/10, 5/−8, and 2/−3 in ascending order:

Solution:

We first write the given rational numbers so that their denominators are positive.

We have,

5/−8 = 5× (−1)/ (−8) × (−1) = −5/8 and 2/−3 = 2× (−1)/ (−3) × (−1) = −2/3

Thus, the given rational numbers with positive denominators are

−7/10, −5/8, −2/3

Now, LCM of the denominators 10, 8 and 3 is 2 × 2 × 2 × 3 × 5 = 120

We now write the numerators so that they have a common denominator 120 as follows:

−7/10= (−7) ×12/10×12= −84/120,

−5/8= (−5) ×15/8×15 = −75/120 and

−2/3= (−2) ×40/3×40 = −80/120

Comparing the numerators of these numbers, we get,

– 84 < -80 < -75

Therefore, −84/120< −80/120< −75/120⇒ −7/10< −2/3< −5/8

⇒ −7/10< 2/−3 < 5/−8

Hence, the given numbers when arranged in ascending order are:

−7/10, 2/−3, 5/−8

2. Arrange the rational numbers 5/8, 5/−6, 7/−4, and 3/5 in ascending order.

Solution:

First, we write each one of the given rational numbers with a positive denominator.

Clearly, denominators of 5/8 and 3/5 are positive.

The denominators of 5/−6 and 7/−4 are negative.

So, we express 5/−6 and 7/−4 with positive denominator as follows:

5/−6 = 5× (−1)/ (−6) × (−1) = −5/6 and 7/−4 = 7× (−1)/ (−4) × (−1) = −7/4

Thus, the given rational numbers with positive denominators are

5/8, −5/6, −7/4 and 3/5

Now, LCM of the denominators 8, 6, 4 and 5 is 2 × 2 × 2 × 3 × 5 = 120

Now we convert each of the rational numbers to their equivalent rational number with common denominator 120 as follows:

5/8 = 5×15/8×15,    

 [Multiplying the numerator and denominator by 120 ÷ 8 = 15]

⇒ 5/8 = 75/120

−5/6= (−5) ×20/6×20,

[Multiplying the numerator and denominator by 120 ÷ 6 = 20]

⇒ −5/6= −100/120

−7/4 = (−7) ×30/4×30,

[Multiplying the numerator and denominator by 120 ÷ 4 = 30]

⇒ −7/4= −210/120 and

 3/5 = 3×24/5×24,     

[Multiplying the numerator and denominator by 120 ÷ 5 = 24]

⇒ 3/5 = 72/120

Comparing the numerators of these numbers, we get,

-210 < -100 < 72 < 75

Therefore, −210/120< −100/120< 72/120 < 75/120

 ⇒ −7/4< −5/6< 3/5 < 5/8 ⇒ 7/−4 < 5/−6 < 3/5 < 5/8

Hence, the given numbers when arranged in ascending order are:

7/−4, 5/−6, 3/5, 5/8.

3. Write the following rational numbers in Ascending Order

 -3/5, -1/5, -2/5

Solution:

Since all the numbers have a common denominator the one with a smaller numerator is the smaller rational number. However, when it comes to negative numbers the higher one is the smaller one.

Therefore, arranging the given rational numbers, we get -3/5, -2/5, -1/5

4. Arrange the rational numbers 1/2, -2/9, -4/3 in Ascending Order?

Solution:

Find the LCM of the denominators 2, 9, 3

LCM of 2, 9, and 3 is 18

Express the given rational numbers with the LCM in terms of common denominator.

1/ 2= 1×9/2×9 = 9/18

-2/9 = -2×2/9×2 = -4/18

-4/3 = -4×6/3×6 = -24/18

Check the numerators of all the rational numbers expressed with a common denominator.

Since -24 is less than the other two we can arrange the given rational numbers in Ascending Order. -24/18, -4/18, 9/18

-4/3, -2/9, 1/2 is the Ascending Order of Given Rational Numbers.

5. Arrange the Rational Numbers 5/8, 4/-6, 3/5 in ascending order?

Solution:

Firstly, express the rational numbers with positive denominators by multiplying with -1

4/-6 = 4× (-1) /-6× (-1) = -4/6

So, find the LCM of the denominators 8, 6, 5

LCM of 8, 6, and 5 is 120

5/8 = 5×15/8×15 = 75/120

-4/6 = -4×20/6×20 = -80/120

3/5 = 3×24/5×24 = 72/120

Check the numerator of the rational numbers having common denominators.

Since -80 is the smallest that itself is the smallest rational number.

Therefore, 4/-6, 3/5, 5/8 are in Ascending Order.

Arrange the Rational Numbers in Descending Order

We will learn how to arrange rational numbers in descending order. The general method is to arrange from the largest to the smallest rational numbers (decreasing): we use the same steps from when we arranged in ascending order

 1: Express the given rational numbers with a positive denominator

2: Take the least common multiple (L.C.M.) of this positive denominator

3: Express each rational number with this least common multiple (LCM) as the common denominator

4: The number having the greater numerator is greater.

Examples:

Example: 1 Arrange the numbers −3/5, 7/−10and −5/8 in descending order.

Solution: First we write each of the given numbers with a positive denominator.

We have;

7/−10 = 7× (−1) / (−10) × (−1) = −7/10.

Thus, the given number is −3/5, −7/10and −5/8.

L.C.M. of 5, 10, and 8 is 40.

Now, −3/5= (−3) ×8/5×8= −24/40;

−7/10= (−7) ×4/10×4= −28/40 And −5/8= (−5) ×5/8×5= −25/40

Clearly, −24/40> −25/40> −28/40

Thus, −35> −5/8> −7/10, i.e., −3/5> −5/8> 7/−10

Hence, the given numbers when arranged in descending order are −3/5, −5/8, and 7/−10.

2. Arrange the following rational numbers in descending order: 4/9, −5/6, −7/−12, and 11/−24.

Solution:

First, we express the given rational numbers in the form so that their denominators are positive.

We have,

−7/−12= (−7) × (−1) / (−12) × (−1) ,

[Multiplying the numerator and denominator by -1]

⇒ −7/−12= 7/12 and

 11/−24= 11× (−1) / (−24) × (−1) = −11/24

Thus, given rational numbers are:

4/9, −5/6, 7/12, −11/24

Now, we find the LCM of 9, 6, 12, and 24.

Required LCM = 2 × 2 × 2 × 3 × 3 = 72.

We now write the rational numbers so that they have a common denominator 72.

We have,

4/9 = 4×8/9×8,

[Multiplying the numerator and denominator by 72 ÷ 9 = 8]

⇒ 4/9 = 32/72

−5/6= −5×12/6×12,

 [Multiplying the numerator and denominator by 72 ÷ 6 = 12]

⇒ −5/6= −60/72

7/12 = 7×6/12×6,

[Multiplying the numerator and denominator by 72 ÷ 12 = 6]

⇒ 7/12 = 42/72

−11/24= −11×3/24×3, [Multiplying the numerator and denominator by 72 ÷ 24 = 3]

⇒ −11/24= −33/72

Arranging the numerators of these rational numbers in descending order, we have

42 > 32 > -33 > -60

 ⇒ 42/72 > 32/72 > −33/72 > −60/72⇒ −7/−12> 4/9 > 11/−24 > −5/6

Hence, the given numbers when arranged in descending order are:

−7/−12, 4/9, 11/−24, −5/6.

3. Arrange the rational numbers −7/10, 5/−8, and 2/−3 in descending order:

Salutation: First we write each one of the given rational numbers with a positive denominator.

We have,

5/−8 = 5× (−1)/ (−8) × (−1) = −5/8 and 2/−3 = 2× (−1)/ (−3) × (−1) = −2/3

Thus, the given rational numbers with positive denominators are

−7/10, −5/8, −2/3

Now, LCM of the denominators 10, 8 and 3 is 2 × 2 × 2 × 3 × 5 = 120

We now write the numerators so that they have a common denominator 120 as follows:

−7/10= (−7) ×12/10×12= −84/120,

−5/8= (−5) ×15/8×15 = −75/120 and

−2/3= (−2) ×40/3×40 = −80/120

Comparing the numerators of these numbers, we get,

-75>-80>-84

Therefore, -75/120 > -80/120 > -84/120 ⇒ -5/8 > -2/3 >-7/10

Hence, the given numbers when arranged in descending order are:

  5/-8 >2/-3 > -7/10

Frequently Asked Questions

Is 0 a rational number?

Yes, 0 is a rational number as it can be written as a fraction of integers like 0/1, 0/-2… Etc.

What defines a rational number?

Any number that can be written as a ratio or fraction of two integers is a rational number.

How many types of rational numbers are there?

There are four types of rational numbers. These are fractions, decimals, integers, terminating decimals and rational numbers.

What is an irrational number?

An irrational number is a real number which cannot be written in the form of a fraction.

In the end, we try to summarize the relationship between the different numbers and the set of rational numbers. This includes all the sets of numbers that you have studied before. We will expand on by learning more about the set of rational numbers, their properties, and the arithmetic operations. Check out our premium courses for children.